Topic 6 Natural BaseLogarithmic and Exponential Functions
This note focuses on the definitions and properties of natural base logarithmic and exponential functions and their applications in business and economics.
6.1 Review: Inverse Function
- Notation Let \(f(x)\) be a strictly monotonic function with domain D and range R. The inverse of \(f(x)\), denoted by \(f^{-1}(x)\), is also a strictly monotonic function with domain R and range D. The following figure uses a simple example to illustrate the the relationship between a function and its inverse.
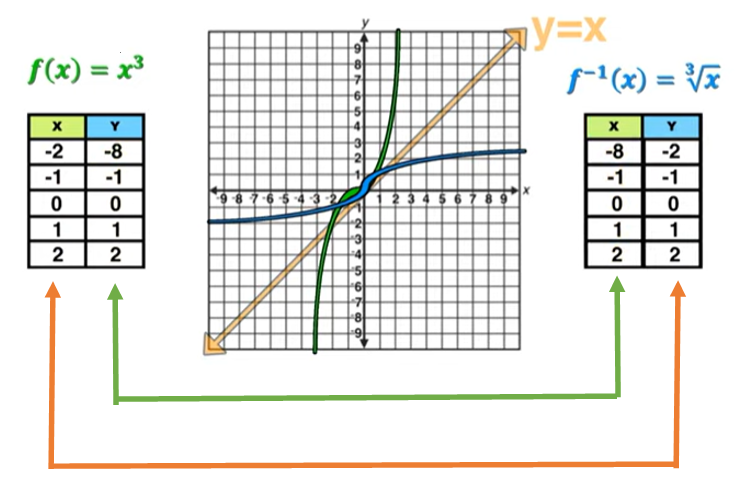
The above table and figure basically show that we swap x- and y-coordinates of one function to get its inverse and the corresponding curves are symmetric with respect to \(y = x\), the diagonal of the first and third quadrants.
Algebraically, the above figure basically says that, to find the inverse of \(y = f(x)\) (if it exists), we only need to swap \(x\) and \(y\) in \(y = f(x)\) to get \(x = f(y)\). Keep in mind that \(y\) in \(x = f(y)\) is still the dependent variable and x is still the independent variable.
In many cases, we want to re-express \(y\) explicitly in term of \(x\) as \(y = f^{-1}(x)\) if the close form exists.
Next chart shows the steps for finding the explicit expression of an inverse function (if it exists).
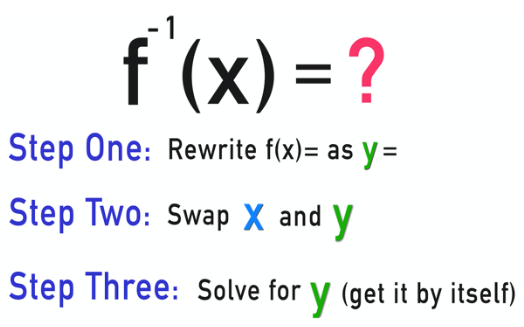
Example 1. Find the inverse function of \(f(x) = x^2\) for \(x > 0\).
Solution: According to the steps, we have
Step 1. let \(y = x^2\).
Step 2. swap \(x\) and \(y\): \(x = y^2\).
Step 3. Solve for \(y\): \(y = \sqrt{x}\).
Therefore, the inverse of \(f(x) = x^2\) is given by \(y = f^{-1}(x) = \sqrt{x}\).
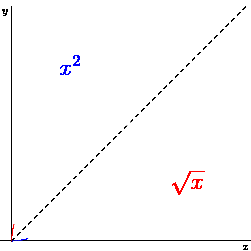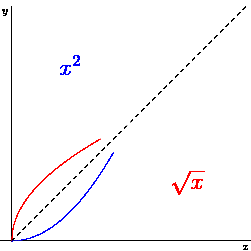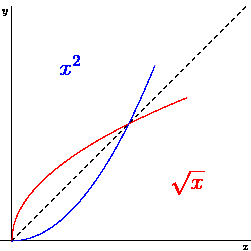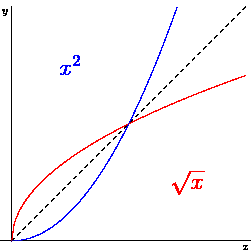
The following animated graph shows the symmetry of \(y = x^2\) and \(x = \sqrt{x}\).
6.2 Definition of Natural Base (Euler Constant \(e\))
Example 2. Assume that you put 10000 dollars (principal, denoted by \(P\)) in a saving account. The Bank pays you the interest at an annual rate of \(r\) (in decimal, for example, \(r = 2.5\% = 0.025\)) . We look at the number of times (\(n\)) the bank calculates the compounding interest in a year and the corresponding interest earnings. For convenience, we use \(A\) to denote the acount balance (the amount in the account after a year, i.e., A = principal + interest).
\(n = 1\): A = principal (P) + interest (\(P\times r\)) = \(P + Pr = P(1+r)\).
\(n =2\): Since the bank will compound the interest two times a year. When calculating the interest, we need to use the semi-annual interest rate (\(r/2\)) instead of the original annual rate (\(r\)).
First calculation: \(A_1 = P + P\times (r/2) = P(1 + r/2)\). Since the interest from every previous period is added to the principal, this means that \(A_1\) will be new principal in the second calculation;
Second calculation: \(A_2 = A_1 + A_1 \times (r/2) = A_1(1+r/2) = P(1+r/2)\times (1 + r/2) = P(1 + r/2)^2\).
\(n = 3\): Use the sample logic in the case of \(n = 2\), the interest rate in each of the three calculations is \(r/3\).
First calculation: \(A_1 = P + P\times (r/3) = P(1 + r/3)\), This \(A_1\) will be new principal in the second calculation;
Second calculation: \(A_2 = A_1 + A_1 \times (r/3) = A_1(1+r/3) = P(1+r/3)\times (1 + r/3) = P(1 + r/3)^2\).
Third calculation: \(A_3 = A_2 + A_2 \times (r/3) = A_2(1+r/3) = P(1+r/3)^2\times (1 + r/3) = P(1 + r/3)^3\).
In general, if the interest is compounded \(n\) times a year, then the balance is expressed in the following
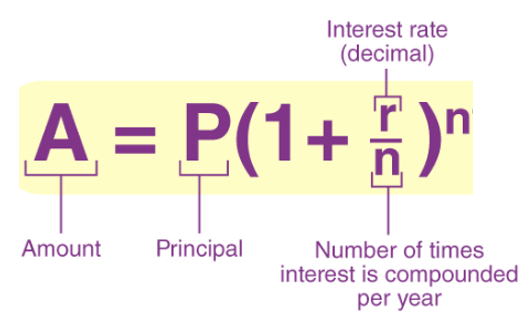
The above formula can be re-expressed into
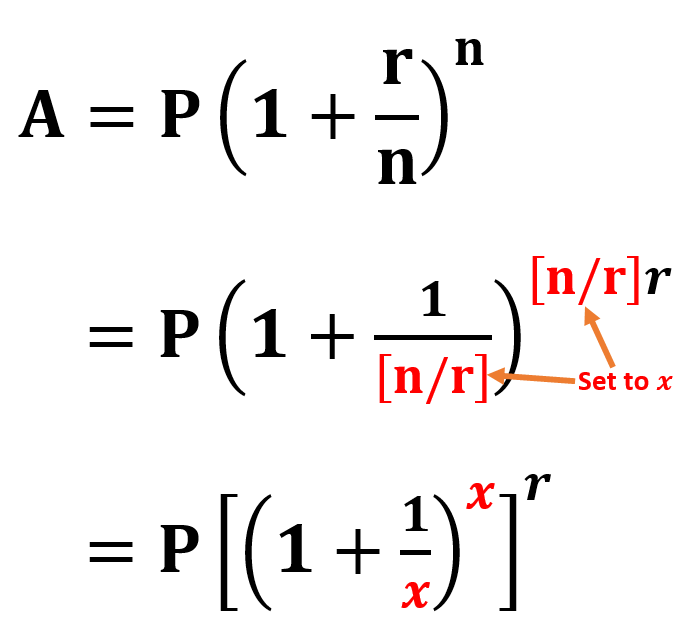
If the interest is compounded continuously, i.e., \(n \to \infty\), then \(x \to \infty\).
Definition: The natural base, denoted by \(e\), is the constant value given by \[ e = \lim_{x \to \infty}\left( 1 + \frac{1}{x}\right)^x \approx 2.71828182845.... \]
Therefore, if the interest is compounded continually, the account balance after a year is simply expressed in the following form
More generally, with principal \(P\) and continuous compounding interest, the account balance after \(y\) years is
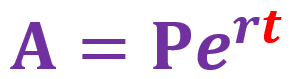where \(t = \text{ number of years}\). The component \(e^r\) is dependent on the value of the nominal annual interest rate. It is considered a function of \(r\) - natural base exponential function.
Example 3: Rachel invests $20,000 in an account that earns interest at an annual rate of 4%. Find the future value of her account after 3 yr if interest is compounded continuously.
Solution: We have \(P =\$20000, r = 0.04\), and \(t = 3\). Since interest is compounded continuously, after 3 yr, Rachel’s account will be worth
\[ A = 20000e^{0.04\times 3} = 23470.22. \] Therefore, the account balance after 3 years is \(\$23470.22\).
6.3 Natural-base Exponential and Logarithmic Functions
The example in the previous section shows that various exponential growth and decay models in applications in the business and other fields are natural base exponential function. Next, we outline the natural base exponential function and its inverse, natural base exponential and logarithmic functions.
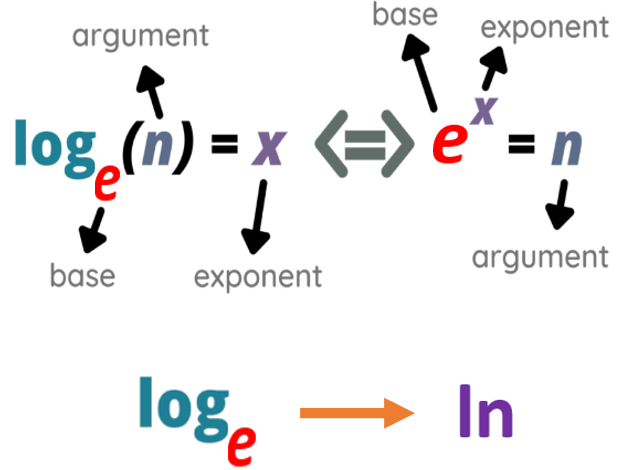
The definition of natural base exponential and longarithmic functions are defined respectively in the following.
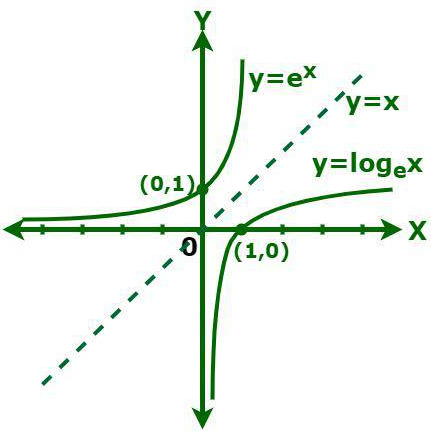
Since \(y = e^x\) and \(y = \ln(x)\) are mutually inverse, their curves are symmetric with respect to \(y = x\).
The basic properties of natural logarithmic and exponential functions are summarized in the following.
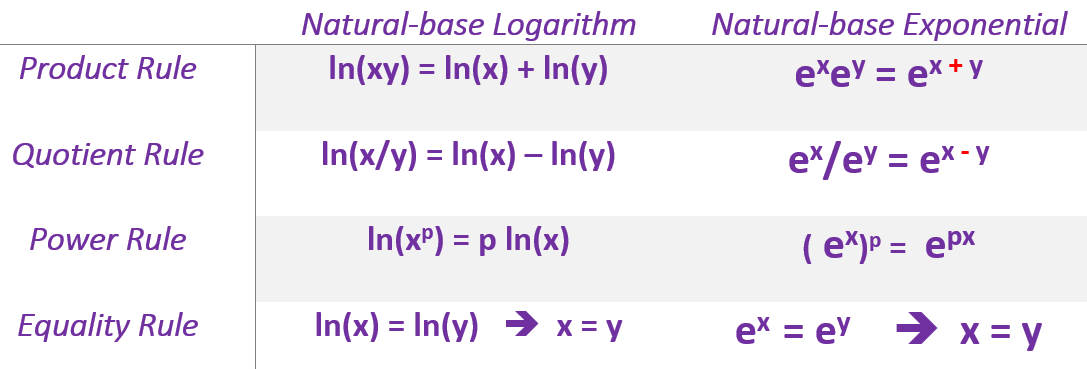
Example 3: Simply the following expressions.
\(\ln(x^4\sqrt{x^5})\)
\(\ln(x^3y^2/z^5)\)
Solution: We the above rules to simply the given expressions.
\(\ln(x^4\sqrt{x^5}) = \ln(x^4 \times x^{5/2}) = \ln(x^{4+5/2}) = \ln(x^{13/2}) = (13/2)\ln(x)\)
\(\ln(x^3y^2/z^5) = \ln(x^3y^2) -\ln(z^5) = \ln(x^3) + \ln(y^2) - \ln(x^5) = 3\ln x+2\ln y -5\ln z\).