Topic 11 Maximum, Minimum and Applications

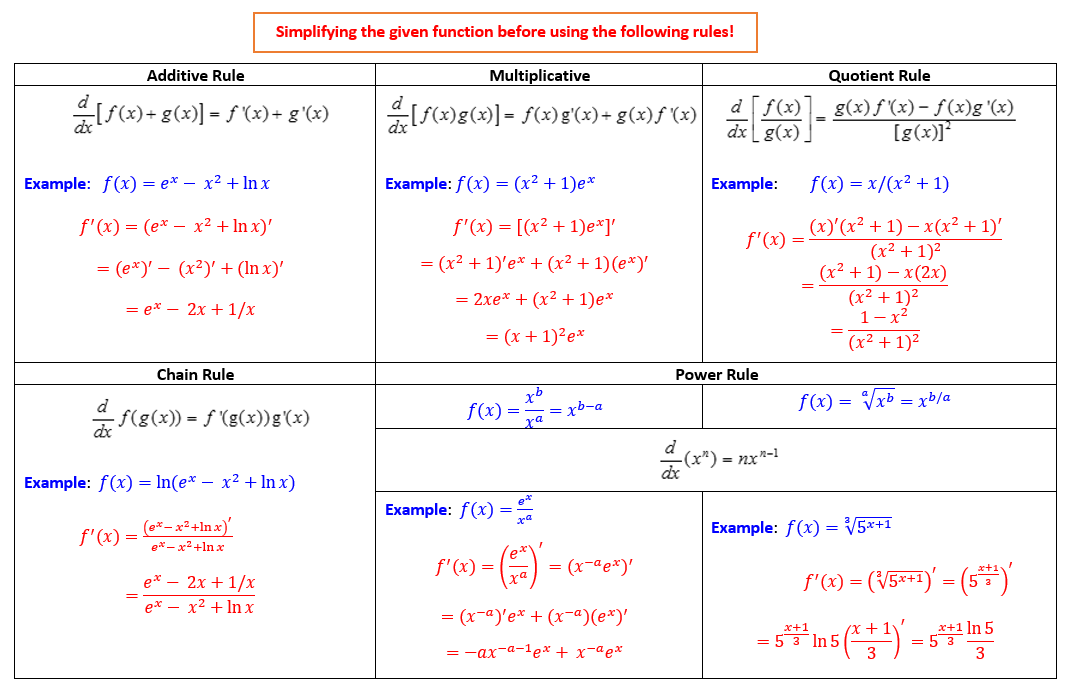
Rules of Derivatives.

Critical Values, Inflection, and Concavity

11.1 Absolute Maximum and Minimum

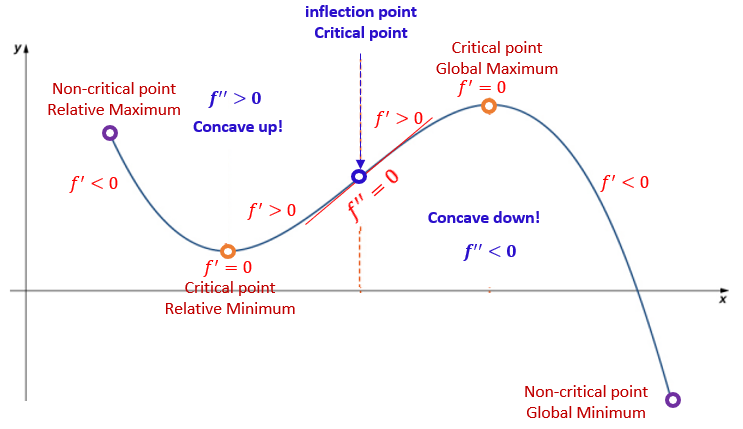
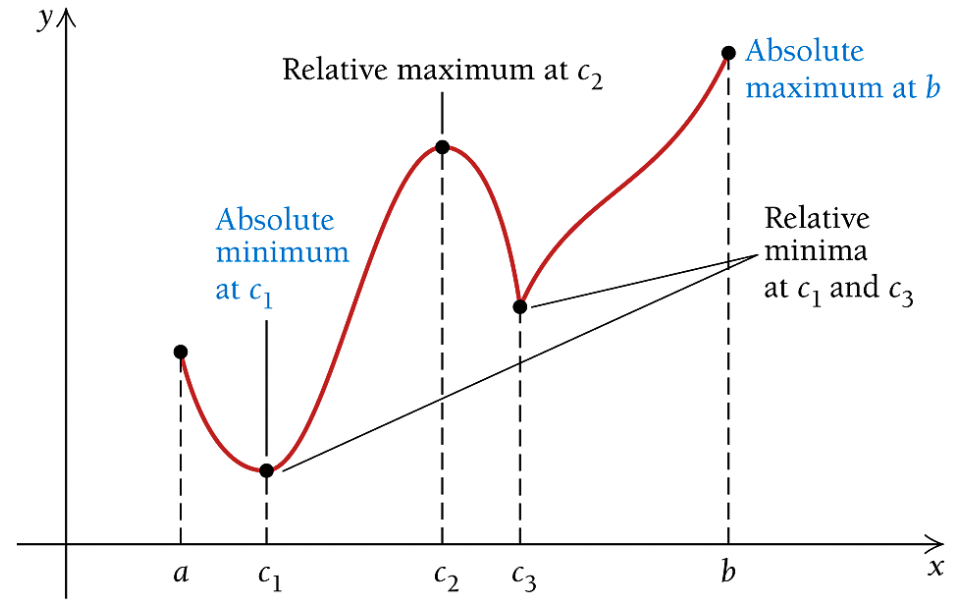
We have described the absolute (global) maximum and minimum in different figures in the previous note. Next, we give the verbal definition of absolute extrema in the following.

Definition: Suppose that $f(x)$ is a function with domain I.

$f(c)$ is an absolute (global) minimum if $f(c) \le f(x)$ for all $x \in I$;
$f(c)$ is an absolute (global) maximum if $f(c) \ge f(x)$ for all $x \in I$;

Example 1: Find the global minimum of function $f(x) = x^2 +1$.

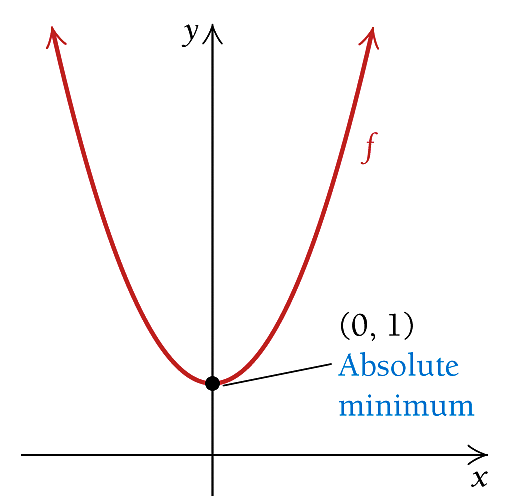
Solution: Since the domain of $f(x)$ is $(-\infty, \infty)$ and there is no global maximum (note $-\infty$ is not a number!), the global minimum must also be a relative minimum. To find the relative minimum, we need only to find the critical value.

\[ f^\prime(x) = 0 ~~\Rightarrow~~ 2x = 0 ~~ \Rightarrow ~~ x = 0. \]

Therefore, the global minimum is $f(0) = 0^2 + 1 = 1$ (see the minimum in the above figure).

11.2 Maximum and Minimum Principles

This section introduces the steps and principles of maximum and minimum.

11.2.1 Steps for Finding Absolute Maximum and Minimum

Suppose $f(x)$ is a continuous function defined over a closed interval $[a, b]$. To find the absolute maximum and minimum values over $[a, b]$, we suggest using the following steps:

Step 1: Find $f^\prime(x)$

Step 2: Determine all critical values in $[a, b]$. By definition, we find all $c$ in $[a, b]$ for which

\[ f^\prime(c) = 0 ~~\text{or}~~ f^\prime(c)~~\text{does not exist}. \]

Step 3: list all values from Step 2 and the endpoints of the interval:

\[ a, c_1, c_2, \cdots, c_n, b. \]

Step 4: Evaluate $f(x)$ for each value in Step 3:

\[ f(a), f(c_1), f(c_2), \cdots, f(c_n), f(b). \]

The largest of these is the absolute maximum of $f(x)$ over $[a, b]$. The smallest of these is the absolute minimum of $f(x)$ over $[a, b]$.

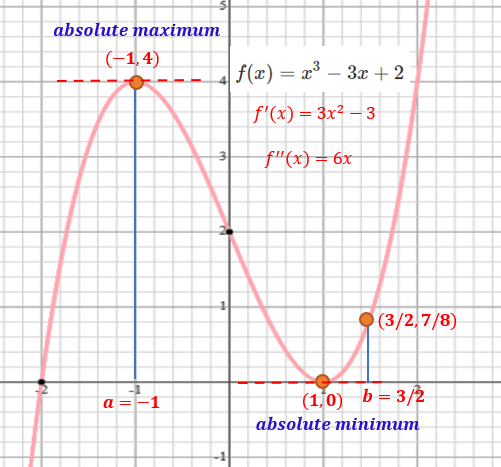
Example 2: Find the absolute maximum and absolute minimum values of \[ f(x) = x^3 - 3x + 2 \]

over interval $[-1, 3/2]$.

Solution: We follow the above steps to identify the absolute minimum and maximum.

Step 1: $f^\prime(x) = [x^3 - 3x + 2]^\prime = (x^3)^\prime - 3(x)^\prime + (2)^\prime = 3x^2 - 3$.

Step 2: Set $f^\prime(x) = 0$ to get $3x^2 - 3 = 0$. Therefore, $3(x^2 -1)= 0$ and $x = 1$ or $x = -1$. Denote $c_1 = 1$ and $c_2 = -1$.

Step 3: The absolute maximum and minimum must be achieved among $a = -1( = c_1), c_2 = 1, 3/2 = b$.

Step 4: Evaluate $f(x) = x^3 - 3x + 2$ at the above three distinct value of $x$: \[ f(-1) = (-1)^3 - 3(-1) + 2 = 4, ~~~ f(1) = 1^3 - 3(1) + 2 = 0,\\ ~~~ f(3/2) = (3/2)^3 - 3(3/2) + 2 = 27/8 - 9/2 + 2 = 7/8. \]

Therefore, the absolute maximum is 4 ($x = -1$) and the absolute minimum is 0 ($x =1$).

11.2.2 Single Absolute Maximum/Minimum Over An Open Interval

Suppose $f(x)$ is a function such that $f^\prime(x)$ exists for every $x$ in an open interval $I$ and the critical value $c$ in $I$, for which $f^\prime(c) = 0$. Then

$f(c)$ is the absolute maximum value over $I$ if $f^{\prime\prime}(c) < 0$.
$f(c)$ is the absolute minimum value over $I$ if $f^{\prime\prime}(c) > 0$

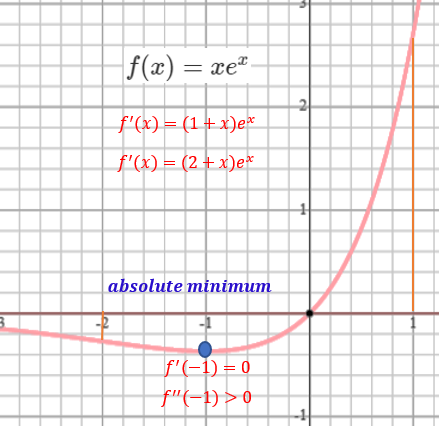
Example 3: Find the absolute extreme value of $f(x) = xe^x$ over interval $(-2, 1)$.

Solution: We first find the critical value on the given interval $(-2, 1)$. \[ f^\prime(x) = [xe^x]^\prime = (x)^\prime e^x + x(e^x)^\prime = e^x + xe^x = (1+x)e^x = 0 \\ ~~\Rightarrow ~~ 1 + x = 0~~\Rightarrow~~ x = -1. \]

To determine whether $f(x)$ achieves it maximum or minimum at $x = -1$, we need the second order derivative

\[ f^{\prime\prime}(x) = [(1+x)e^x]^\prime = (1+x)^\prime e^x + (1+x)(e^x)^\prime = e^x + (1+x)e^x = (2+x)e^x, \]

Note that \[ f^{\prime\prime}(-1) = (2-1)e^{-1} = e^{-1} \approx 0.367879441171442 > 0. \]

Therefore, $f(x) = xe^x$ achieves its absolute minimum at $x = -1$.

11.3 Business Applications

In this section, we will demonstrate how derivatives are used in business applications using various examples.

11.3.1 Minimization of Average Cost

Assume that $C(x)$, $R(x)$, and $P(x)$ are cost, revenue, and profit functions respectively. Note that $P(x) = R(x) - C(x)$.

Average cost function is defined as $\overline{C(x)} = C(x) / x$.
Average revenue function is defined as $\overline{R(x)} = R(x) / x$.
Average profit function is defined as $\overline{P(x)} = P(x) / x$.

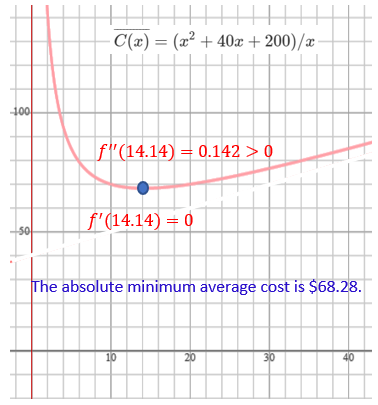
Example 4: Average Cost The cost of materials, C, in dollars, to produce $x$ dozen birthday cakes at Yum’s Bakery is given by \[ C(x) = x^2 + 40 x + 200 \] 1. Find the average cost, $\overline{C(x)} = C(x)/x$.

Solution: By the definition, the average cost is given by \[ \overline{C(x)} = (x^2 + 40 x + 200)/x = x + 40 + 200/x. \]

Find the minimum average cost and interpret the result.

Solution. The domain of the average cost function is $(0, \infty)$. We first find the critical value of the average cost function. \[ [\overline{C(x)}]^\prime = [x + 40 + 200/x]^\prime = (x)^\prime + (40)^\prime + [200x^{-1}]^\prime \\ = 1 -200x^{-2} = 1-\frac{200}{x^2} = \frac{x^2-200}{x^2} \]

Setting $[\overline{C(x)}]^\prime = 0$, we have

\[ \frac{x^2-200}{x^2} ~~\Rightarrow~~ x^2 - 200 = 0. ~~~\text{Therefore, } x = \sqrt{200} \approx 14.14. \]

\[ [\overline{C(x)}]^{\prime\prime} = [1 -200x^{-2} ]^\prime = (1)^\prime - 200(x^{-2})^\prime = -(200)\times(-2x^{-2-1}) = 400x^{-3} \]

\[ [\overline{C(14.12)}]^{\prime\prime} = 400\times 14.12^{-3} \approx 0.142 > 0. \] Therefore $\overline{C(x)}$ is concave down. The minimum average cost is

\[ \overline{C(14.14)} = 14.14 + 40 + 200/14.14 \approx 68.28. \]

11.3.2 Minimizing Manufacturing Cost

Example 5: Minimizing Manufacturing Cost Mendoza Manufacturers specializes in food-storage containers and makes a cylindrical soup can with a volume of 250 cm3.

The cost of material for the two circular ends is $0.0008/$cm^2$, and the cost of material for the side is $0.0015/cm2. What dimensions minimize the cost of material for the soup can? What is the minimum cost?

Solution: First, we cut the can in the following way to obtain two circles and one rectangle and then calculate the total area.

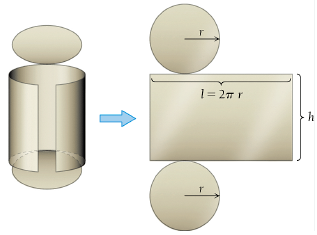
The cost of the material for the side area \[ C_{\text{side}} = \text{Area} \times \text{unit price} = 2\pi r h \times 0.0015 = 0.003\pi rh \] Similarly, the cost of the material for the two circular ends is

\[ C_{\text{ends}} = \text{Area} \times \text{unit price} = 2\pi r^2 \times 0.0008 = 0.0016\pi r^2 \]

Note that a cylinder with base radius $r$ and height $h$ has volume

\[ V = \text{base area } \times \text{ height} = \pi r^2 \times h \]

For the specific can in this example with volume 250, we have $250 = \pi r^2h$, that is $h = 250/(\pi r^2)$. Therefore, the cost function is defined by

\[ C(r) = 0.0016\pi r^2 + 0.003\pi r \times \frac{250}{\pi r^2} = 0.0016\pi r^2 + \frac{0.75}{r} \]

Next, we use the minimum and maximum principles and steps to find the minimum cost based on the above steps.

Step 1: $C^\prime(r) = [0.0016\pi r^2 + \frac{0.75}{r}]^\prime = 0.0016\pi (r^2)^\prime + \left[\frac{0.75}{r}\right]^\prime$$=0.0032\pi r -\frac{0.75}{r^2}$.

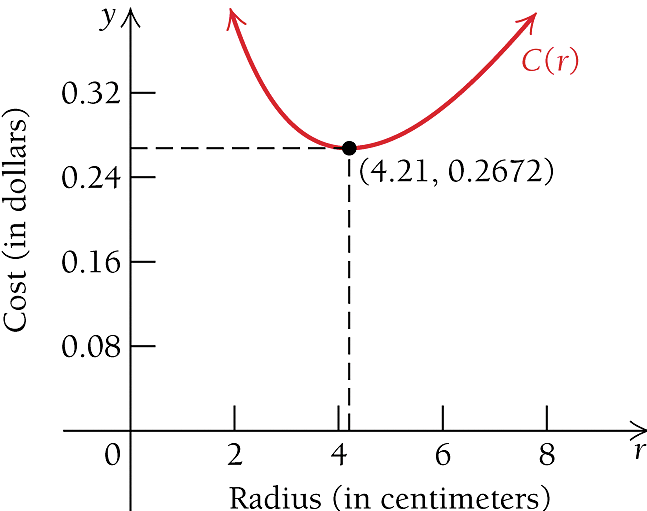
Step 2: Setting $C^\prime(r) = 0$, we have \[ 0.0032\pi r -\frac{0.75}{r^2} = 0~~\Rightarrow~~0.0032\pi r^3 = 0.75~~\Rightarrow~~ r =\sqrt[3]{\frac{0.75}{0.0032\pi}} \approx 4.209726 \]

Step 3: Find the second-order derivative to determine minimum/maximum.

\[ C^{\prime\prime}(r) = 0.0032\pi (r)^\prime - \left( \frac{0.75}{r^2}\right)^\prime = 0.0032\pi - 0.75(r^{-2})^\prime \\ = 0.0032\pi - 0.75 \times (-2)r^{-2-1} = 0.0032\pi + 1.5 r^{-3} \]

Step 4: Since $C^{\prime\prime}(4.21) = 0.0032\pi + 1.5\times 4.21^{-3} \approx 0.03015536 > 0$, the cost function achieves it minimum at $r = 4.21$. The minimum cost is

\[ C(4.21) = 0.0016\pi r^2 + \frac{0.75}{r} = 0.0016\pi \times 4.21^2 + \frac{0.75}{4.21} \approx 0.2672383 \]

### Maximizing Profit

Example 5: Cruzing Tunes determines that in order to sell $x$ units of a new car audio receiver, the price per unit, in dollars, must be

\[ p(x) = 1000 - x. \] It also determines that the total cost of producing $x$ units is given by \[ C(x) = 3000 + 20x. \] A). Find the total revenue, $R(x)$.

B). Find the total profit. $P(x)$.

C). How many units must be made and sold in order to maximize profit?

D). What is the maximum profit?

Solution:

A). Since the unit sale price is $p(x) = 1000-x$. Therefore, the revenue from selling x units is \[ R(x) = x\times p(x) = x(1000-x) = 1000x - x^2. \]

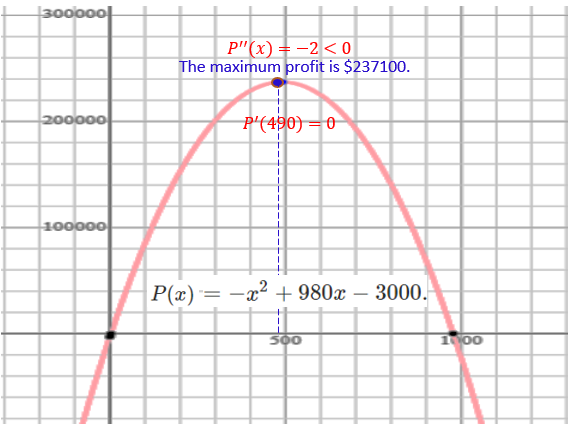
B). According to the relationship between $C(x)$, $R(x)$, and $P(x)$, we have profit function \[ P(x) = R(x) - C(x) = 1000x - x^2 -(3000 + 20x) = -x^2 + 980x - 3000. \]

C). We need the first and second-order derivatives to find the critical value(s) and the concavity of $P(x)$. \[ P^\prime(x) = [-x^2 + 980x - 3000]^\prime = -2x + 980 \] Setting $P^\prime(x) = 0$, we have $-2x + 980 = 0$ which gives $x = 490$. Note that $P^{\prime\prime}(x) = (-20x + 980)^\prime = -2 < 0$. The profit achieves its maximum when producing $x = 490$ items.

D). The maximum profit is $P(490) =-(490)^2 + 980\times 490 - 3000 = 237100$ dollars.