Topic 13 Definition of Antiderivative
13.1 Review: Rules of Derivative
- Rules of Derivatives.
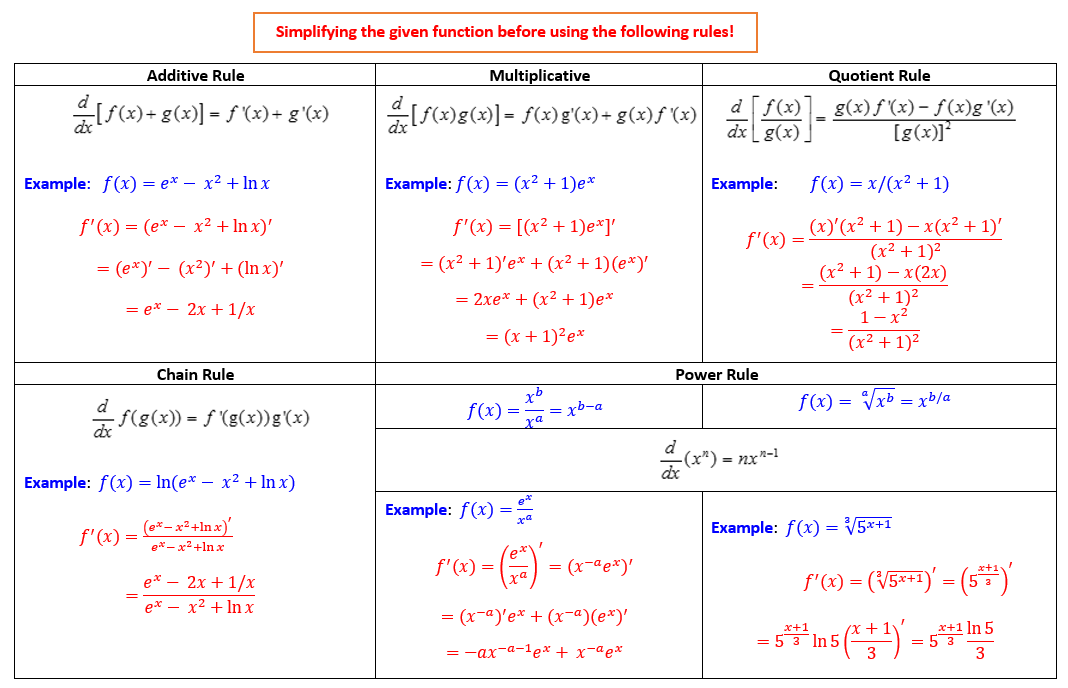
- Derivative of Some Specific Simple Functions
\[ \begin{array}{llcl} \text{1. Identity function} & \frac{d(x)}{dx} & = & 1 \\ \text{2. Linear function} & \frac{d(ax)}{dx} & = & a \\ \text{3. Power function} & \frac{d(x^k)}{dx} & = & kx^{k-1} \\ \text{4. Natural base logarithmic function} & \frac{d(\ln x)}{dx} & = & \frac{1}{x} \\ \text{5. Natural base exponential function} & \frac{d(e^x)}{dx} & = & e^x \\ \text{6. General logarithmic function} & \frac{d(\log_a x)}{dx} & = & \frac{1}{x\ln a} \\ \text{7. General exponential function} & \frac{d(a^x)}{dx} & = & a^x\ln a \\ \end{array} \]
In this and the next few notes, we introduce the concept and applications of integral (integration). The process of finding the integral is the opposite process of differentiation. The concept of integration is also practically important.
For example, for every unit of product sold, a company accumulates profit. We can use the method of integration to find cumulative profit. The profit from selling a unit of product is called marginal profit (which is the derivative of profit). Before introducing the related concepts of integration and their applications, we need to use the concept of the antiderivative.
13.2 Anti-derivative
First, we look at the relationship between the following two functions
\[ F(x) = x^2 + C ~~~\text{and}~~~ f(x) = 2x. \] Clearly,
\[ \frac{d}{dx}F(x) = (x^2+c)^\prime = (x^2)^\prime + (C)^\prime = 2x = f(x)! \] In other words, \(f(x)\) is the derivative of \(F(x)\). We define \(F(x)\) to be an antiderivative of \(f(x)\)! The process of finding anti-derivative is called antidifferentiation.
Because \(F(c)\) contains a constant \(C\), that means, for a given function \(f(x)\), its antiderivative IS NOT UNIQUE!
13.2.1 Finding Antiderivatives
The process of differentiation is performed in reverse. Given a function \(f(x)\), we find another function \(F(x)\) such that
\[ \frac{d}{dx}F(x) = f(x). \]
The antiderivative of \(f(x)\) is the set of functions \(F(x) + C\) such that
\[ \frac{d}{dx}\left[ F(x) + C\right] = f(x). \] The constant \(C\) is called the constant of integration.
Important notation: If \(F(x)\) is an antiderivative of \(f(x)\), we write
\[ \int f(x) = F(x) + C. \] This equation is read as the antiderivative of f(x), with respect to \(x\), is \(F(x) + C\) or as the integral of \(f(x)\), with respect to \(x\), is \(F(x) + C\) The expression on the left side is called an indefinite integral. The symbol \(\int\) is the integral sign, and \(f(x)\) is the integrand. The symbol \(dx\) can be regarded as indicating that \(x\) is the variable of integration, similar to \(d/dx\) indicating that the expression that follows it is to be differentiated with respect to \(x\).
13.2.2 Rules of Integration
The following gives the integral of the most commonly used functions. We will use these basic integrals to calculate the integral of many other functions.

The following two properties of integration are used along with the basic integral in the above table to calculate the integral of other functions with more complex forms.
- Additive Rule:
\[\int [f(x) \pm g(x)] dx = \int f(x) dx \pm \int g(x) dx\].
- Scalar Multiplication Rule:
\[\int Df(x) dx = D\int f(x) dx \].
Example 1: Find the following integrals.
\(\int (1/x^3) dx\).
\(\int \sqrt{x} dx\).
\(\int (e^{-3x}) dx\).
Solution: We use the result in the above integration table to find the integrals.
- We first rewrite the integrand into the form of a power function and then use the integration table to find the integral.
\[ \int \frac{1}{x^3} dx = \int x^{-3} dx = \frac{x^{-3 + 1}}{-3 + 1} + C = -\frac{1}{2x^2} + C. \]
- Re-express the radical function as a power function and then use the integral of the power function.
\[ \int \sqrt{x} dx = \int x^{1/2} dx = \frac{x^{1/2+1}}{1/2 + 1} + C = \frac{x^{3/2}}{3/2} + C = \frac{2x^{3/2}}{3} + C. \]
- We can use the integral of \(e^{ax}\) to find the desired integral.
\[
\int (e^{-3x}) dx = \frac{1}{-3}e^{-3x} + C = -\frac{1}{3}e^{-3x} + C.
\]
Example 2: Find the integral of the following functions.
\(f(x) =3x^5 + 7x^3 + 8\).
\(f(x) = (4 + 3x + 2x^4)/x\)
Solution: We use the additive and power rule to find the integral of the following functions.
- Using the additive property, scalar multiplication, and the power rule.
\[ \int f(x)dx =\int(3x^5 + 7x^3 + 8)dx = 3\int x^5 dx + 7\int x^3 dx + 8\int 1 dx \] \[ = 3 \frac{x^{5+1}}{5+1} + 7\frac{x^{3+1}}{3+1} + 8 x + C = \frac{x^6}{2} + \frac{7x^4}{4} + 8x +C. \]
- Note that \(f(x) = (4 + 3x + 2x^4)/x = 4x^{-1} + 3 + 2x\).
\[ \int f(x) dx = \int (4/x + 3 + 2x) dx = 4\int \left( \frac{1}{x}\right)dx + 3\int 1 dx + 2\int x dx \]
\[ = 4\ln |x| + 3x +2\frac{x^{1+1}}{1+1}+C = 4\ln|x| + 3x + x^2 + C. \]